La regresión lineal es una técnica estadística utilizada en el campo de la psicología para analizar la relación entre una variable dependiente y una o más variables independientes. Esta herramienta nos permite predecir o estimar el valor de la variable dependiente en función de los valores de las variables independientes.

Qué es la regresión lineal y para qué sirve
En el contexto del machine learning, los algoritmos de regresión lineal analizan grandes conjuntos de datos para calcular la ecuación de regresión lineal. Estos algoritmos se entrenan con conjuntos de datos conocidos o etiquetados, y luego se utilizan para predecir valores desconocidos.
Para que la regresión lineal sea adecuada, se deben cumplir ciertos supuestos. En primer lugar, debe existir una relación lineal entre las variables independientes y la variable dependiente. Esto se determina mediante la creación de una gráfica de dispersión, donde se evalúa si los puntos caen a lo largo de una línea recta. En caso contrario, es posible que se requiera aplicar transformaciones matemáticas para lograr una relación lineal.
Otro supuesto fundamental es que los residuos, que son las diferencias entre los valores observados y los valores predichos, deben ser independientes entre sí. Esto significa que no debe haber un patrón identificable en los residuos, como un incremento o decremento sistemático a lo largo del tiempo.
Además, los residuos deben seguir una distribución normal, lo cual se evalúa mediante técnicas de representación gráfica como las gráficas Q-Q. Si los residuos no siguen una distribución normal, se pueden detectar valores atípicos o realizar transformaciones para corregir este problema.
Por último, se asume que los residuos tienen una variación constante o desviación estándar de la media para cada valor de la variable independiente. Si esta suposición no se cumple, es posible que sea necesario realizar cambios en la variable dependiente o en la escala de la misma.
Modelo de regresión lineal
El modelo de regresión lineal se puede expresar mediante la siguiente ecuación:
y = β0 + β1*x1 + β2*x2 + ... + βn*xn + ε
Donde:
- y es la variable dependiente que queremos predecir o estimar.
- β0 es el término de intersección o constante.
- β1, β2, ..., βn son los coeficientes de regresión que indican la relación entre cada variable independiente y la variable dependiente.
- x1, x2, ..., xn son las variables independientes.
- ε es el término de error o residuo.
El objetivo de la regresión lineal es encontrar los valores óptimos de los coeficientes de regresión para minimizar la suma de los cuadrados de los residuos. Esto se conoce como el método de los mínimos cuadrados.
Una vez obtenida la ecuación de regresión lineal, podemos utilizarla para predecir el valor de la variable dependiente para nuevos valores de las variables independientes. Esto es especialmente útil en el campo de la psicología, donde podemos utilizar la regresión lineal para predecir el rendimiento académico, la satisfacción laboral, la salud mental, entre otros aspectos relevantes.
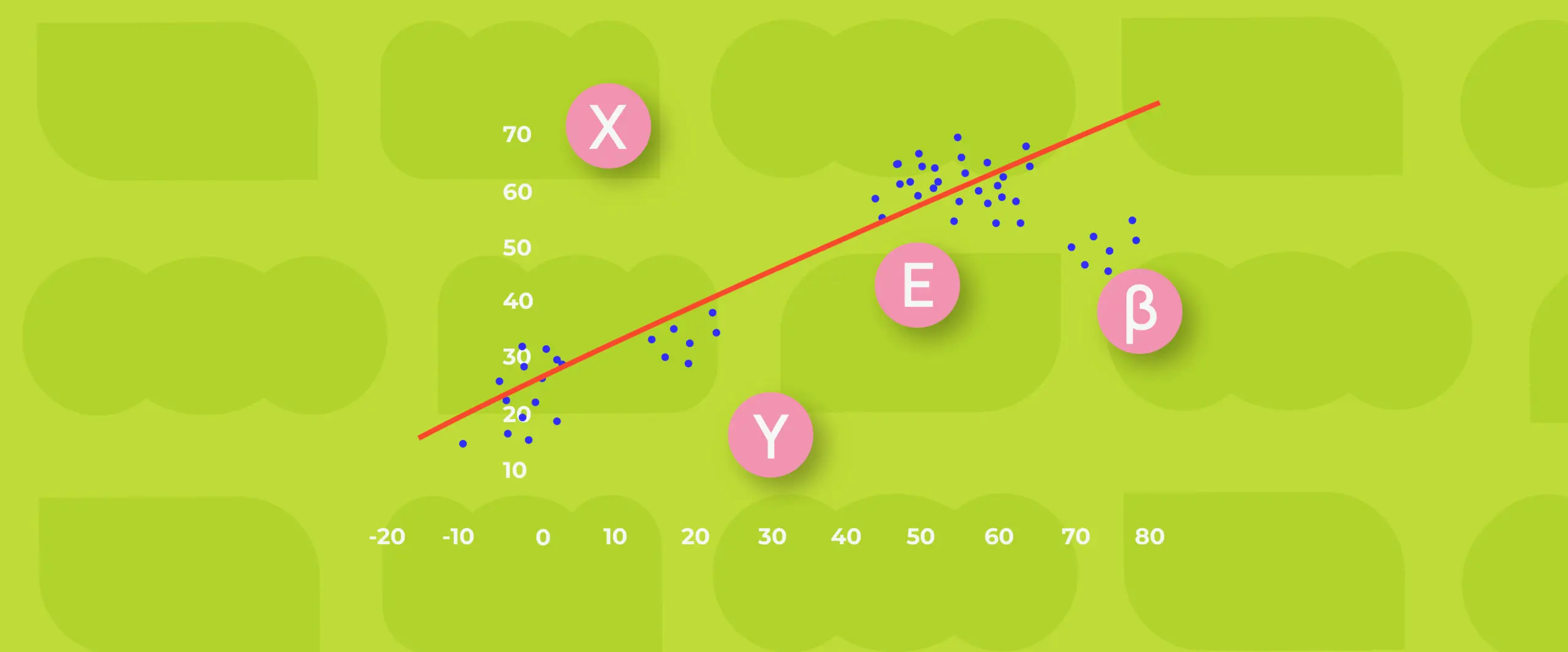
Regresión no lineal en psicología
Aunque la regresión lineal es una herramienta poderosa, en algunos casos la relación entre las variables puede ser no lineal. En estos casos, se utiliza la regresión no lineal, que permite modelar relaciones más complejas entre las variables.
La regresión no lineal utiliza funciones matemáticas no lineales para modelar la relación entre las variables. Algunos ejemplos de funciones no lineales comunes son la exponencial, logarítmica, polinómica, sigmoidal, entre otras.
En psicología, la regresión no lineal puede ser útil para analizar relaciones más complejas, como la curva de aprendizaje, el efecto de dosis-respuesta en el consumo de drogas, la relación entre la edad y la memoria, entre otros.
Para ajustar un modelo de regresión no lineal, se utilizan técnicas de optimización para encontrar los valores óptimos de los parámetros de la función no lineal. Estas técnicas buscan minimizar la diferencia entre los valores observados y los valores predichos por el modelo.
Tanto la regresión lineal como la regresión no lineal son herramientas fundamentales en el análisis de datos en psicología. La regresión lineal nos permite analizar relaciones lineales entre variables, mientras que la regresión no lineal nos permite modelar relaciones más complejas. Ambas técnicas nos ayudan a comprender y predecir el comportamiento humano en diferentes contextos.
Consultas habituales
¿Cuándo debo utilizar la regresión lineal en psicología?
La regresión lineal es útil cuando queremos analizar la relación lineal entre una variable dependiente y una o más variables independientes. Se utiliza en psicología para predecir o estimar valores de variables como el rendimiento académico, la satisfacción laboral, la salud mental, entre otros.
¿Cuándo debo utilizar la regresión no lineal en psicología?
La regresión no lineal se utiliza cuando la relación entre las variables no es lineal. Es útil en psicología para modelar relaciones más complejas, como la curva de aprendizaje, el efecto de dosis-respuesta en el consumo de drogas, la relación entre la edad y la memoria, entre otros.
¿Cuáles son los supuestos de la regresión lineal en psicología?
Los supuestos de la regresión lineal en psicología incluyen: relación lineal entre las variables, independencia residual, normalidad de los residuos y homocedasticidad. Estos supuestos deben ser evaluados y, si no se cumplen, se deben aplicar técnicas de transformación o considerar otros modelos.
¿Cómo puedo evaluar la calidad de un modelo de regresión lineal en psicología?
Existen diferentes métricas para evaluar la calidad de un modelo de regresión lineal en psicología, como el coeficiente de determinación (R²), el error estándar de la estimación (SEE), el análisis de la varianza (ANOVA), entre otros. Estas métricas nos permiten determinar qué tan bien se ajusta el modelo a los datos observados.
La regresión lineal y la regresión no lineal son herramientas fundamentales en el análisis de datos en psicología. La regresión lineal nos permite analizar relaciones lineales entre variables, mientras que la regresión no lineal nos permite modelar relaciones más complejas. Ambas técnicas nos ayudan a comprender y predecir el comportamiento humano en diferentes contextos. Tener en cuenta los supuestos de la regresión lineal y evaluar la calidad del modelo para asegurarnos de obtener resultados confiables y significativos.
Si quieres conocer otros artículos parecidos a Regresión lineal en psicología: análisis de datos puedes visitar la categoría Psicología.

